8.1 Introduction

La géométrie sphérique est la géométrie obtenu lorsque l’on travaille sur la surface d’une sphère. Une telle géométrie est particulièrement importante du moment que l’on réalise que notre planète est une sphère. Il s’agit d’une géométrie particulièrement utile, entre autre dans le domaine de la navigation. Dans ce cas, il est nécessaire de redéfinir plusieurs des concepts de base de la géométrie.

—

Un segment entre $A$ et $B$ est le plus court trajet (sur la sphère) entre ces deux points.
—

Une droite est le prolongement dans les deux directions d’un segment.

Dans ce cas, comme nous allons le démontrer très bientôt, on remarque qu’une droite sphérique a la particularité de n’être rien d’autre que l’un des grands cercles de la sphère, c’est à dire l’une des circonférences de la sphère. Notez que le complément d’un segment sur une droite est parfois aussi appelé un segment, bien qu’il ne soit pas le plus court trajet entre deux points. Nous allons cependant normalement éviter de le faire pour éviter de rencontrer des difficultés dans la définition de nos triangles.

Une fois la notion de segment définie, on peut alors parler de triangle sphérique. Il s’agit alors, comme en géométrie euclidienne, d’une figure géométrique ayant trois sommets, et pour laquelle chacun des sommets est relié entre eux par un segment. Les triangles sphériques possèdent possèdent plusieurs propriétés particulièrement différente de celle que nous rencontrons en géométrie euclidienne. Par exemple, comme nous le verrons un peu plus tard dans le chapitre, en géométrie sphérique la somme des angles d’un triangle est toujours strictement supérieure à 180^o. De plus, le critère de similitude AAA devient un critère de congruence. Voici un exemple de triangle sphérique.

En géométrie sphérique, et plus précisément en trigonométrie sphérique, nous dénoterons pour les lettres majuscules $A,B,C$ les trois sommets d’un triangle sphérique, et en même temps les angles formés à ces sommets. Pour ce qui est des côtés, nous les dénoterons par les lettres minuscules correspondantes $a,b,c$ , et prenant pour convention que $a$ est le côté opposé au sommet $A$ , $b$ est le côté opposé au sommet $B$ , et de même pour $c$ et $C$ . De plus, par convention, toute les mesures seront donnés en degré (ou en radian), ce qui inclut la mesure des côtés. La mesure d’un segment $AB$ sera donc l’angle au centre $\angle AOB$ où $O$ est le centre de la sphère. Ceci a l’avantage de rentre les équations indépendante du rayon de la sphère. Remarquez qu’il est facile de convertir entre unités de longueur (cm / m) et unités d’angle (degré / radian) à partir de la formule suivante:

\frac{x_{\textrm{cm}}}{\textrm{circonf\'{e}rence}}=\frac{x_{\textrm{degr\'{e}}% }}{360}=\frac{x_{\textrm{radian}}}{2\pi}

Théorème 8.1.1:

Segment sphérique. En géométrie sphérique, tous les segments se trouve sur un grand cercle. De plus, toutes les droites sont des grands cercles et vice-versa.

Démonstration.

La démonstration proposé ci-dessous a été proposé par Sylvie Dornez, une ancienne étudiante du cours de géométrie.

1.

Prenons deux points, A et B, sur une sphère de rayon R et centrée en O.
2.

Considérons le plan qui contient les points A, B et O, disons le plan 1 (voir Figure 8.1). Le cercle dans ce plan est un grand cercle, car le cercle a le même rayon que la sphère, R. Aussi, ce grand cercle (comme tous les grand cercles) est centré en O.

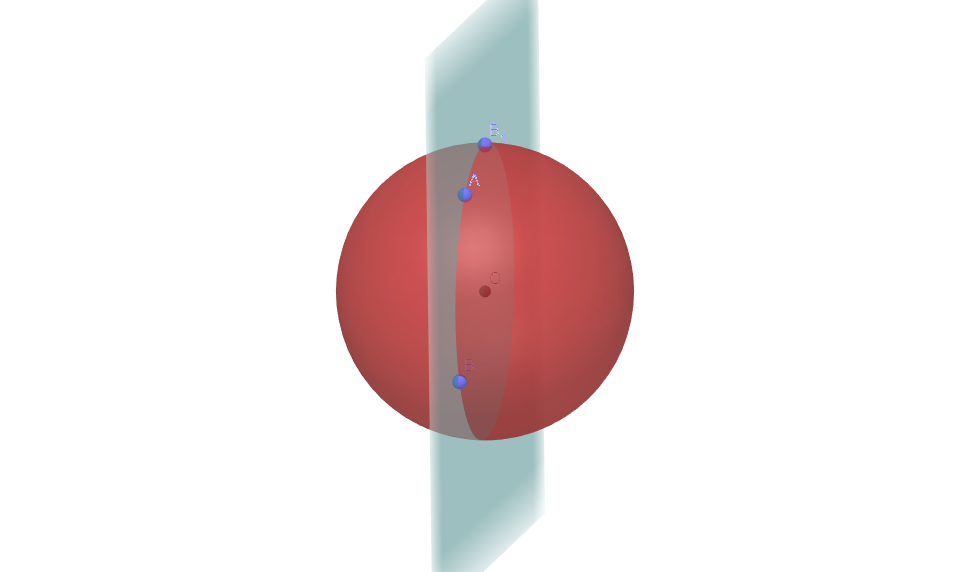
Figure 8.1: Plan 1

Considérons également le plan qui passe par A, B et C, disons le plan 2 (voir Figure 8.2), où C est un point quelconque de la sphère qui ne se situe pas dans le plan 1. Le cercle dans ce plan a un rayon qui est plus petit que R, disons r. Dénotons son centre par P.

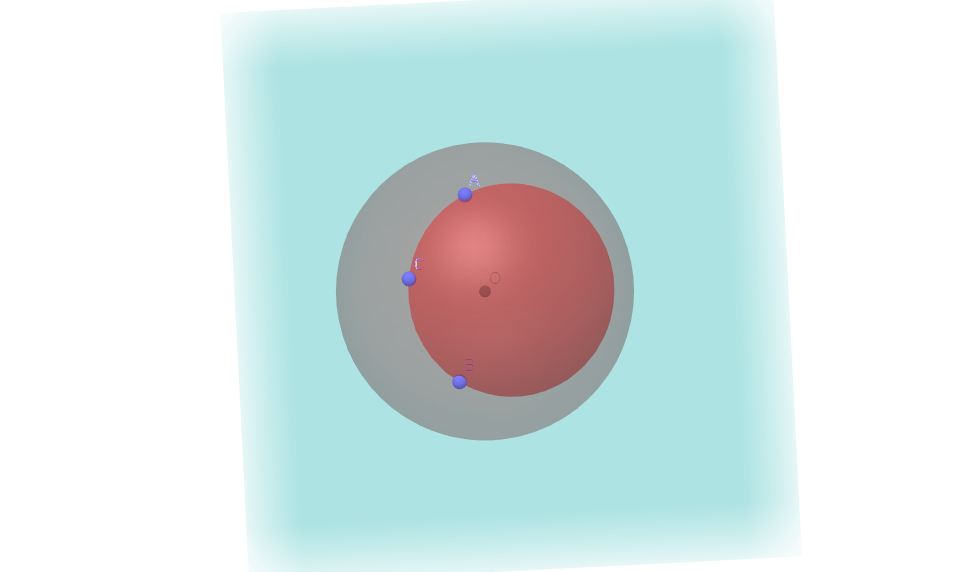
Figure 8.2: Plan 2
3.

Le segment AB, au sens euclidien, forme une corde à ces deux cercles. De plus, ce même segment AB sert de base pour deux triangles isocèles $\triangle{AOB}$ et $\triangle{APB}$ , ayant pour côtés les rayons, R et r respectivement. À partir de ces triangles isocèles, on peut voir que $\angle{AOB}<\angle{APB}$ .
4.

Il reste à remarquer que ces angles sont en effet la mesure en radian des arcs AB des cercles identifiés à l’étape 2. Donc l’arc AB sur le cercle centré en O est plus court que l’arc AB sur le cercle centré en P. Donc le plus court trajet entre A et B se trouve sur un grand cercle.

∎

À remarquer que le théorème précédent a plusieurs conséquences importantes. En particulier, deux droites distinctes ont toujours exactement $2$ points d’intersection, ce qui signifie qu’il n’existe pas de droite parallèle. De plus, par deux points passent toujours exactement une droite, sauf si ces deux points sont opposés sur la sphère (par exemple pôle nord et pôle sud). Dans ce cas il y a une infinité de droites passant par ces deux points.