Chapitre 1 Une petite histoire des mathématiques
La géométrie est l’étude des figures. Avec l’arithmétique, il s’agit de l’une des branches des mathématiques les plus anciennes. On retrouve des traces de connaissance géométrique dès la préhistoire sous forme de dessins, certains datés d’environ avant Jésus-Christ. La géométrie précède donc de plusieurs millénaires l’invention de l’écriture. C’est justement l’absence d’écriture qui rend l’étude de la géométrie préhistorique particulièrement difficile, ce qui explique que très peu est connu à ce sujet.
La Mésopotamie
Les mathématiques mésopotamiennes commencent à se développer vers 3000 avant Jésus-Christ dans la civilisation sumérienne. On y retrouve alors des tables de multiplication, ainsi que des énoncés de certains problèmes de géométrie écrits sur des tablettes d’argile. C’est cependant la civilisation babylonienne (2000 à 1600 avant J.-C.) qui les suivit et qui nous laissa la majorité des artéfacts de la Mésopotamie ancienne. C’est à partir d’un ensemble d’environ 400 tablettes d’argile que nous pouvons inférer leur connaissance mathématique. L’un des aspects les plus connus des mathématiques de la Mésopotamie est un système de nombres en base 60 qui est parvenu jusqu’à nous par l’intermédiaire des mesures d’angles en degrés, ou bien de la division d’une heure en 60 minutes. Les mathématiques de la Mésopotamie étaient principalement d’un aspect pratique, appliqué par exemple au commerce ou à l’agriculture. Ils calculaient la circonférence d’un cercle en multipliant son diamètre par 3, et étaient conscients du théorème de Pythagore.



L’Égypte ancienne
Environ au même moment que les Babyloniens, les Égyptiens développent aussi des connaissances considérables en mathématiques, possiblement complètement indépendamment des peuples de la Mésopotamie. Il y a cependant très peu de documents attestant de leur connaissance qui ont survécu jusqu’à nous, étant donné que le papyrus utilisé en Égypte est beaucoup plus fragile que les tablettes d’argile des Mésopotamiens. Les deux papyrus les plus importants d’un point de vue des mathématiques sont le papyrus de Moscou qui contient un ensemble de 25 problèmes avec leur solution, et le papyrus Rhind qui en contient 87. Ces deux papyrus s’intéressent entre autres à l’arithmétique et à la géométrie dans un objectif pratique lié en particulier à l’agriculture ou aux taxes. La légende indique qu’après chaque crue du Nil, il fallait reconstituer les parcelles, ce qui aurait en partie motivé l’étude de la géométrie.
Parmi les résultats trouvés dans ces textes, on peut noter entre autres que l’aire d’un triangle isocèle est égale à sa hauteur multipliée par la moitié de sa base, ce qui est bien entendu vrai, mais on retrouve aussi que l’aire d’un quadrilatère quelconque est le produit de la moitié des sommes des côtés opposés, ce qui est complètement faux. Les résultats des Égyptiens étaient basés essentiellement sur l’observation. Ils ne faisaient pas la distinction entre résultat exact et approximation. Ils ont pourtant réussi à obtenir correctement plusieurs résultats particulièrement impressionnants pour l’époque, comme une formule exacte pour le calcul du volume d’une pyramide.


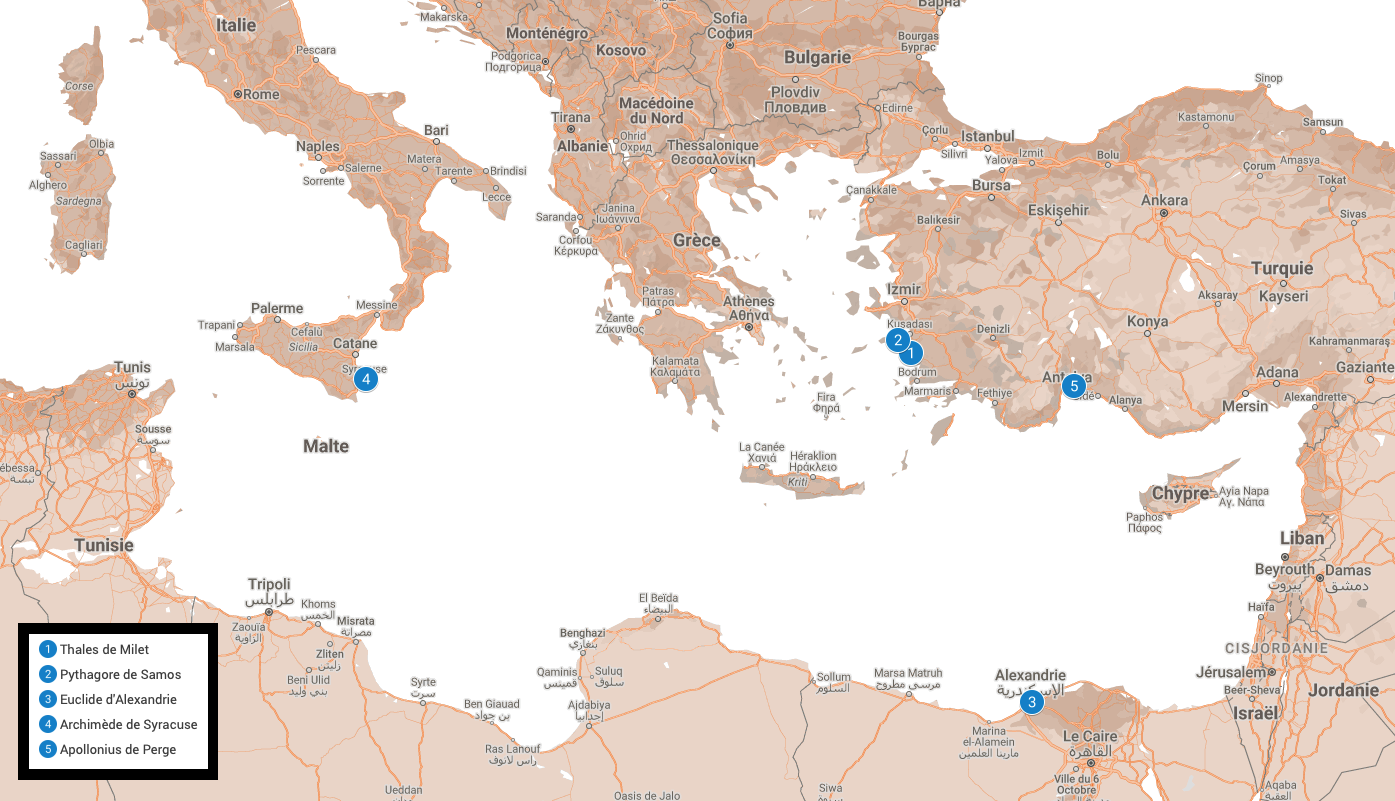
Thalès de Milet (Environ 625 à 545 avant J.-C.)
C’est avec Thalès de Milet que tout va commencer à changer. Thalès est un philosophe et mathématicien de la Grèce antique né à Milet dans la Turquie actuelle aux environs de 625 avant Jésus-Christ, et serait décédé aux environs de 545 avant Jésus-Christ dans cette même ville. À la suite d’un voyage en Égypte, et peut-être aussi en Mésopotamie, il aurait acquis de nombreuses connaissances sur les mathématiques de ces deux civilisations. Contrairement à ses prédécesseurs, il ne se contente pas d’observer, mais se demande aussi pourquoi les résultats sont valides. Il est parfois crédité d’avoir écrit la première démonstration de l’histoire, ce qui lui donne le titre de Premier mathématicien. Bien qu’il n’ait laissé aucune trace écrite, il a profondément marqué l’histoire des sciences et aurait appartenu aux sept sages de la Grèce antique.
Pythagore de Samos (Environ 570 à 500 avant J.-C.)
Pythagore est né à Samos, une île de la mer Égée appartenant à la Grèce, au sud-est de la ville d’Athènes tout près des côtes de la Turquie. Il est l’une des figures les plus connues des mathématiques antiques, en particulier du au théorème qui porte son nom. Bien que le théorème fût connu plusieurs siècles avant lui, c’est Pythagore et son école qui en auraient fourni la première démonstration. Pythagore, ou plutôt l’école des Pythagoriciens qu’il a fondée et avec laquelle il est particulièrement difficile de le différencier, développe un mysticisme des nombres. Il s’agit en fait d’un culte (ou religion) basé sur un caractère mystique associé à chaque nombre. Le un est à la base des nombres, il est donc associé à Dieu (Zeus). Le nombre deux pour sa part représentait le féminin, alors que le nombre trois représentait le masculin. Le nombre cinq représente le mariage, car il s’agit de la somme de deux et trois. Finalement, le nombre six est parfait, car il s’agit de la somme de ses diviseurs propres (1+2+3=6). La signification des nombres selon Pythagore peut nous sembler particulièrement étrange, mais a pourtant joué un rôle fondamental dans l’histoire des mathématiques. C’est en effet ce côté mystique qui a motivé l’étude des mathématiques par les Pythagoriciens. Pythagore cherche à utiliser les nombres (à comprendre ici les nombres rationnels) comme fondement de toutes les mathématiques de son époque. Ceci s’avèrera cependant un échec après que l’un de ses disciples eût démontré que 2 n’est le carré d’aucun nombre rationnel. Un tel nombre devrait pourtant exister en appliquant le théorème de Pythagore à un triangle rectangle pour lequel chacune de ses cathètes est de longueur 1.
Euclide d’Alexandrie (Environ 365 à 300 avant J.-C.)
Les mathématiques continuent de se développer rapidement dans la Grèce antique, mais c’est sans aucun doute Euclide qui les marquera le plus, malgré le fait que très peu est connu sur sa vie. Euclide cherchait à établir les mathématiques sur une base solide, tout comme Pythagore l’avait fait avant lui. Il prend cependant une approche radicalement différente. Alors que Pythagore avait essayé d’utiliser l’arithmétique comme fondement des mathématiques et avait échoué, Euclide choisit plutôt d’utiliser la géométrie. Pour ce faire, Euclide choisit un ensemble de 5 axiomes (ou postulats) qu’il supposera vrais sans démonstration, et qu’il utilisera ensuite pour démontrer l’essentiel des mathématiques connu à son époque. C’est le début de la méthode axiomatique, une méthode qui a profondément marqué l’histoire et qui est maintenant utilisée dans toutes les branches des mathématiques. Dans ce cours, nous reprendrons l’approche axiomatique d’Euclide, en utilisant une notation plus moderne. Euclide est connu pour un ensemble de 13 volumes dénommé Les Éléments, qui contient un nombre considérable de résultats de géométrie et d’arithmétique. Ces livres formeront partie du cursus universitaire standard jusqu’au début du XXe siècle. Il s’agit de l’un des premiers livres ayant été imprimés et du deuxième livre ayant connu le plus grand nombre d’éditions, dépassé uniquement par la bible. Il faut insister sur le fait que le génie d’Euclide ne réside pas dans la quantité de résultats qu’il a découverts, car un grand nombre étaient connus avant lui, mais plutôt dans la méthode qu’il a développée et la rigueur de son traitement.





Archimède de Syracuse (Environ 287 à 212 avant J.-C.)
Archimède est un autre des plus grands noms des mathématiques ou même des sciences en général. Il est originaire de Syracuse en Sicile, une colonie de la Grèce antique qui fait aujourd’hui partie de l’Italie. Contrairement à Euclide qui est surtout connu pour le développement d’une méthode théorique, Archimède s’intéresse surtout à des problèmes appliqués pour lesquels il apporte une contribution considérable. Parmi ses plus grandes contributions mathématiques, on peut noter entre autres le développement de la méthode d’exhaustion, une méthode précurseur du calcul intégral qu’Archimède a développée près de 2000 ans avant la naissance de Newton et Leibniz. Cette méthode lui permettra de faire de nombreuses découvertes en lien avec les calculs d’aire et de volume pour entre autres le cercle et la sphère, mais aussi pour la parabole. Il obtient par la même occasion des résultats concernant le nombre pi. Selon la légende, il serait décédé lors de la prise de Syracuse par les Romains. Très concentré sur des problèmes de géométrie, il aurait dit à un soldat romain de ne pas déranger ses cercles, ce qui aurait vexé le soldat qui aurait tué le vieillard d’un coup d’épée.
Apollonius de Perge (Environ 262 à 190 avant J.-C.)
Apollonius est probablement le dernier des grands noms de l’âge d’or des mathématiques de la Grèce antique. Né à Perge dans l’actuelle Turquie, il continue dans la même lignée qu’Euclide et écrira de nombreux traités que l’on peut voir comme une suite des éléments. Malheureusement, plusieurs d’entre eux n’ont pas survécu jusqu’à nous et ils ne nous sont connus que par des sources indirectes. Son traité le plus connu est celui des coniques dans lequel il étudie de nombreuses propriétés de l’ellipse, de la parabole et de l’hyperbole. On peut aussi noter son traité des contacts dans lequel il s’intéresse à construire à la règle et au compas un cercle tangent à trois objets choisis parmi des points, des droites et des cercles. Ces 10 constructions (sans inclure les cas particuliers) joueront un rôle important dans les chapitres à venir.
La fin de l’âge d’or des mathématiques grecque
Après Apollonius, c’est le début du déclin de la géométrie dans la Grèce antique. Il y aura bien entendu d’autres développements importants, mais les nouveaux travaux notables se font de plus en plus distants. Les résultats les plus importants de la fin de la période grecque concernent principalement le développement de la trigonométrie plane, mais aussi sphérique. Cette dernière étant celle qui se développera en premier motivée par l’étude de l’astronomie. Parmi les mathématiciens d’importance, on peut par exemple noter Héron (10-70 après J.-C.) qui développe une formule permettant de calculer l’aire d’un triangle à partir de la longueur de ses trois côtés, contrairement à la formule classique qui utilise la base et la hauteur. Vient ensuite Ménélaus (70-130 après J.-C.), qui développera les premiers théorèmes de trigonométrie en utilisant une fonction analogue au sinus que l’on appelle parfois la fonction corde. Ce dernier reste cependant plus connu pour le théorème qui porte maintenant son nom et qui permet de vérifier si trois points associés à un triangle se trouvent sur une même droite. Les travaux de Ménélaus seront par la suite continués par Ptolémée (90-168 après J.-C.) qui écrira ce qui est sans aucun doute la meilleure référence de l’antiquité concernant l’astronomie, ce qui l’amènera à développer des tables trigonométriques extrêmement précises pour son époque. C’est d’ailleurs ce dernier qui effectuera les plus grandes contributions au développement des théorèmes de trigonométrie. Finalement, le titre du dernier des grands mathématiciens de l’antiquité est souvent attribué à Pappus qui établira les bases de la géométrie projective plusieurs siècles avant la découverte de cette dernière.
Renaissance de la géométrie
Pendant des siècles après la chute de la Grèce antique, le développement de la géométrie sera presque au point mort. Cela ne veut pas dire que les mathématiques ne continueront pas à se développer, mais cette fois il faut chercher à l’extérieur de l’Europe. Durant le moyen-âge, ce sont les mathématiciens arabes qui joueront un rôle particulièrement important. Premièrement en important et traduisant de nombreux textes de l’antiquité, ce qui contribuera à les préserver, mais aussi en développant une toute nouvelle branche des mathématiques: l’algèbre. Les problèmes d’algèbre n’étaient pas inconnus des Grecs, mais ces derniers cherchaient à résoudre les équations à partir de problèmes géométriques, alors que les Arabes pourront les résoudre indépendamment. Il faut noter que les mathématiciens perses sont généralement inclus dans les mathématiciens arabes, bien qu’ils soient de langue et culture très différentes. Ceci est dû au fait que la plupart des textes savants issus de la Perse (Iran) étaient rédigés en arabe, au même titre que la plupart des textes savants de l’Europe étaient écrits en latin ou en grec.
Arrive ensuite la renaissance en Europe et la redécouverte de plusieurs textes et connaissances de l’antiquité. On peut par exemple noter Fibonacci qui introduira les nombres arabes en Europe, qui utilisait alors encore les chiffres romains, très peu pratiques au développement des mathématiques. Ceci ne sera cependant pas sans opposition. En ce qui concerne la géométrie, c’est René Descartes (1596-1650), mathématicien français, qui apportera une contribution majeure: l’introduction d’un système de coordonnées. C’est le début de la géométrie cartésienne. Bien que techniquement toujours de la géométrie euclidienne, car satisfaisant les 5 axiomes d’Euclide, cette nouvelle saveur de la géométrie permet d’appliquer toute la puissance de l’algèbre à la géométrie.
Viendra ensuite beaucoup plus récemment l’introduction des vecteurs dans l’étude de la géométrie, ce qui donnera naissance à la géométrie vectorielle. Cette dernière aura l’avantage de rendre la géométrie indépendante de la dimension, mais ajoutera une couche supplémentaire d’abstraction. L’introduction de la géométrie cartésienne, puis de la géométrie vectorielle, permettra de simplifier de plus en plus certaines démonstrations ou calculs, mais s’éloignera en même temps de plus en plus des raisons fondamentales et de l’intuition permettant d’expliquer pourquoi un résultat est correct. La géométrie synthétique, bien que n’étant plus nécessairement la plus répandue, restera tout de même aux yeux de plusieurs la plus élégante.
Ailleurs dans le monde
Bien que ce soient sans aucun doute les mathématiciens de la Grèce antique, tels qu’Euclide, qui auront la plus grande influence sur le développement de la géométrie telle que nous la connaissons aujourd’hui, il ne faut pas oublier qu’ailleurs dans le monde, la géométrie s’est elle aussi développée de manière indépendante. Parmi les travaux les plus considérables, on ne peut passer à côté des mathématiques chinoises qui auront une grande influence sur les mathématiques japonaises et coréennes, mais resteront pendant longtemps presque inconnues en occident. Le document le plus notable des mathématiques chinoises est sans aucun doute le livre « Les neuf chapitres sur l’art mathématique », qui jouera en Asie un rôle similaire à celui « Des éléments » en Europe. Ce texte anonyme écrit par plusieurs générations de mathématiciens entre le 10e siècle avant J.-C. et le 2e siècle après J.-C. cherche à trouver les solutions les plus générales pour résoudre certains problèmes appliqués. Il s’agit en effet d’un recueil de problèmes appliqués contenant pour chacun d’eux une explication de la méthode de solution (forme de démonstration), et une méthode pour effectuer le calcul. Ceci est un contraste important avec la méthode axiomatique des Grecs qui s’intéressait plutôt à développer des résultats abstraits à partir non pas de problèmes appliqués, mais plutôt d’axiomes. Parmi les points les plus importants de ce recueil, on peut y retrouver des classiques de la géométrie comme le théorème de Pythagore, connu sous le nom de théorème de Gou Gu en Asie, mais aussi des méthodes de résolution qui ne feront leur apparition en Europe que plusieurs siècles plus tard, telles que la méthode de complétion du carré et la méthode d’élimination de Gauss.
Parmi les autres civilisations d’importance, il ne faut pas oublier de mentionner l’Inde qui est à l’origine des nombres tels que nous les connaissons aujourd’hui, ou bien la civilisation Maya en Amérique centrale qui développera un système de nombres en base 20, ainsi qu’un calendrier particulièrement remarquable permettant de prédire plusieurs phénomènes astronomiques. Une étude complète des mathématiques de chacune des civilisations importantes de l’histoire dépasserait cependant largement le but de ce recueil. Ce qui est le plus important d’un point de vue historique est l’importance et l’influence qu’auront les travaux des mathématiciens de la Grèce antique, en particulier la méthode axiomatique d’Euclide, sur les développements ultérieurs. Dans le reste du texte, nous allons donc nous concentrer à développer la géométrie selon cette approche.